De
esta manera se obtendrá la trayectoria del misil en cada coordenada (x, y) de
su dominio,
vamos a definir un dominio arbitrario de x [3, 4] y con estos
datos realizaremos una
tabulación de dichos datos.
Al realizar la gráfica,
tenemos como resultado una cóncava o parábola hacia
abajo:
ECUACIÓN CUADRÁTICA
DEFINICIÓN
Una ecuación cuadrática es una ecuación en su
forma ax2 + bx + c.
Donde a, b, c son números reales.
La condición de que a es un número diferente
de cero en la definición asegura que exista el término x2 en la ecuación. Existen varios métodos para resolver las
ecuaciones cuadráticas.
Pero
este tipo de ecuación puede presentarse de diferentes formas:
Ejemplos:
9x2
+ 6x + 10 = 0 a = 9, b = 6, c = 10
3x2 – 9x +
0 = 0 a = 3, b = –9, c = 0 (el cero, la c, no se escribe, no está)
–6x2 + 0x + 10 = 0 a = -6, b = 0, c = 10 (el cero equis, la
b, no se escribe)
El
método apropiado para resolver una ecuación cuadrática depende del tipo de
ecuación cuadrática que se va a resolver y para eso puede usarse cualquiera de
los siguientes métodos:
1. Factorización.
Cuando
un polinomio es igual a cierto valor (ya sea un entero u otro polinomio), el
resultado es una ecuación. Una ecuación que puede ser escrita de la forma ax2 + bx + c = 0. Podemos resolver estas ecuaciones cuadráticas usando las reglas del álgebra, aplicando
técnicas de factorización donde sea necesario, y usando la Propiedad Cero de la
Multiplicación.
2.
La Propiedad Cero de la Multiplicación
La
Propiedad Cero de la Multiplicación establece algo que todos siempre hemos
sabido: si el producto de dos números es 0, entonces por lo menos uno de los
factores es 0.
Esta
propiedad puede parecer obvia, pero tiene importante implicaciones en cómo
resolvemos ecuaciones cuadráticas: significa que si tenemos un polinomio
factorizado igual a 0, podemos estar seguros de que al menos uno de sus
factores es también 0. Podemos usar este método
para identificar soluciones de
una ecuación.
Ejemplo:
Resolver x2
– 5x + 6 = 0.
podemos resolver todas las ecuaciones
cuadráticas por factorización porque este método está limitado a coeficientes enteros. Por eso tenemos que conocer
otros métodos.
3. Completando el cuadrado.
Convierte un polinomio en un trinomio cuadrado
perfecto, el cual es más fácil
de graficar y resolver. Esto es, trinomios de la
forma: x2 + bx.
Regla para hallar el último término de x2
+ bx
El
último término de un trinomio cuadrado perfecto, es el cuadrado de la mitad
del
coeficiente del término del medio:
Completando
el Cuadrado.- Para
completar el cuadrado en una expresión de
la forma x2 + bx,
sumar. Y la expresión se vuelve.
4.
Ecuación Cuadrática
Una ecuación cuadrática es una ecuación en su
forma ax2 + bx + c, donde a, b, c son números reales.
La condición de que a es un número diferente
de cero en la definición asegura que exista el término x2 en la ecuación. Existen varios métodos para resolver las
ecuaciones cuadráticas.
Pero este tipo de ecuación puede presentarse
de diferentes formas:
Ejemplos:
9x2 + 6x + 10 = 0 a = 9, b = 6, c = 10
3x2 – 9x +
0 = 0 a = 3, b = –9, c = 0 (el cero, la c, no se escribe, no está)
–6x2 + 0x + 10 = 0 a = -6, b = 0, c = 10 (el cero equis, la
b, no se escribe)
El método apropiado para resolver una
ecuación cuadrática depende del tipo de ecuación cuadrática que se va a
resolver y para eso puede usarse cualquiera de los siguientes métodos:
5. Factorización.
Cuando un polinomio es igual a cierto valor
(ya sea un entero u otro polinomio), el resultado es una ecuación. Una ecuación
que puede ser escrita de la forma ax2
+ bx + c = 0.
Podemos resolver estas ecuaciones cuadráticas
usando las reglas del álgebra, aplicando técnicas de factorización donde sea
necesario, y usando la Propiedad Cero de la Multiplicación.
6.
La Propiedad Cero de la Multiplicación
La Propiedad Cero de la Multiplicación
establece algo que todos siempre hemos sabido: si el producto de dos números es
0, entonces por lo menos uno de los factores es 0.
Esta propiedad puede parecer obvia, pero
tiene importante implicaciones en cómo resolvemos ecuaciones cuadráticas:
significa que si tenemos un polinomio factorizado igual a 0, podemos estar
seguros de que al menos uno de sus factores es también 0.
Podemos usar este
método para identificar soluciones de una ecuación.
Ejemplo:
Resolver:
x2
– 5x + 6 = 0.
Nota: No podemos resolver todas las ecuaciones cuadráticas por
factorización porque este método está limitado a coeficientes enteros. Por eso tenemos que conocer otros métodos.
7. Completando el cuadrado.
Convierte un polinomio en un trinomio cuadrado
perfecto, el cual es más fácil de graficar y resolver. Esto es, trinomios de la
forma: x2 + bx.
Regla para hallar el último término de x2
+ bx.- El
último término de un trinomio cuadrado perfecto, es el cuadrado de la mitad del
coeficiente del término del medio:
Completando
el Cuadrado.- Para completar el cuadrado
en una expresión de la
forma x2 + bx,
sumar . Y la expresión se vuelve . Y la expresión se vuelve . .
Demostración de la Fórmula Cuadrática o Fórmula General.- Algunos casos la descomposición en factores
de la expresión cuadrática puede presentar dificultades: aún más, en muchos
casos puede sencillamente no haber factores reales. En consecuencia, el método más útil para
resolver una ecuación cuadrática es mediante la llamada fórmula
cuadrática. Obtenemos esta fórmula completando el cuadrado al igual que en la determinación de vértices de la parábola.
Demostración: Si dividimos por el coeficiente de x 2 en la ecuación
anterior y pasamos el término constante al segundo miembro de la ecuación, Podemos completar el cuadrado
en el primer miembro sumando a
ambos miembros de la ecuación:
Extrayendo
raíz cuadrada resulta
Tomando en un caso el signo más y en el otro el signo
menos obtenemos las dos raíces de la ecuación
cuadrática ax2 + bx + c = 0 lo cual completa la demostración. Usted
debe de verificar que cada una de las raíces es en realidad una solución de la
ecuación substituyéndola en: ax2 + bx + c = 0.
Veamos unos ejemplos:
EJERCICIOS PROPUESTOS
6.- Ejercicios propuestos: Ecuaciones
EJERCICIOS PROPUESTOS: Factorization Simple
EJERCICIOS PROPUESTOS: Gráficas
2)
Grafica la función f x = - 1 2 x + 2 2 + 8
x 2 ⇒ 1 2 × x 2
3)
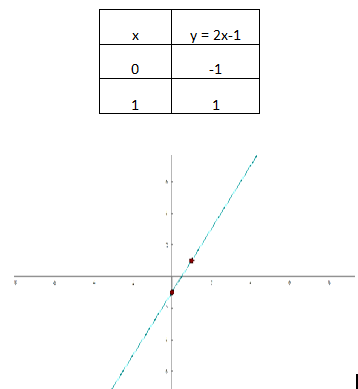
y = 2x − 1
4) Tiene
pendiente −3 y ordenada en el origen −1.
y =
−3x −1
5) f x = x 2
La gráfica de la
función: f x = x 2 es la siguiente:
Bibliografía:
http://www.vitutor.com/fun/1/a_a.html ( EJERCICIOS
PROPUESTOS)
|


















No hay comentarios:
Publicar un comentario